1. झुकने की प्रक्रिया को समझना: सरल तथ्य
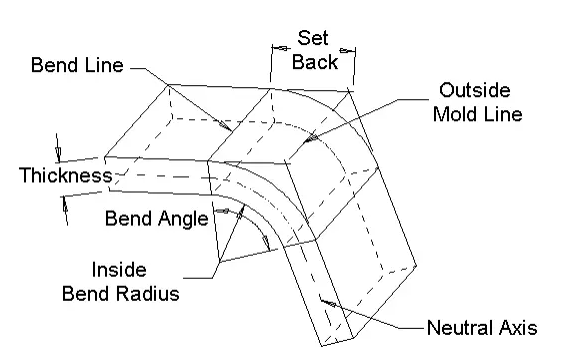
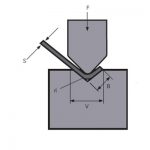
बेंड भत्ता = कोण * (टी / 180) * (त्रिज्या + के-कारक * मोटाई) बेंड मुआवजा = बेंड भत्ता- (2 * वापस सेट करें)
इनसाइड सेट बैक = टैन (कोण/2) *रेडियस आउटसाइडसेट बैक = टैन (कोण/2)*(त्रिज्या + मोटाई)

1) मुड़े हुए भाग पर प्राप्त त्रिज्या उस भाग को काटने की लंबाई को प्रभावित करती है (झुकने से पहले)।
2) झुकने पर प्राप्त त्रिज्या उस वी उद्घाटन पर 99% निर्भर करती है जिसके साथ हम काम करना चाहते हैं।
भाग को डिजाइन करने से पहले और निश्चित रूप से रिक्त स्थान को काटना शुरू करने से पहले, हमें वास्तव में पता होना चाहिए कि प्रेस ब्रेक पर भाग को मोड़ने के लिए हम किस वी उद्घाटन का उपयोग करेंगे।
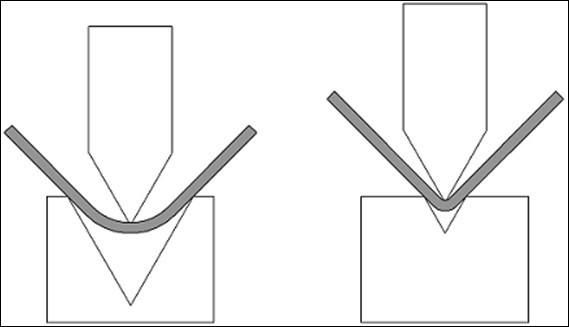
2. त्रिज्या रिक्त स्थान को कैसे प्रभावित करती है
एक बड़ा त्रिज्या हमारे हिस्से के पैरों को बाहर की ओर "धक्का" देगा, जिससे यह आभास होगा कि रिक्त "बहुत लंबा" कट गया था।
एक छोटे त्रिज्या के लिए एक रिक्त स्थान की आवश्यकता होगी जिसे त्रिज्या के बड़े होने की तुलना में "थोड़ा लंबा" काटा जाना चाहिए।
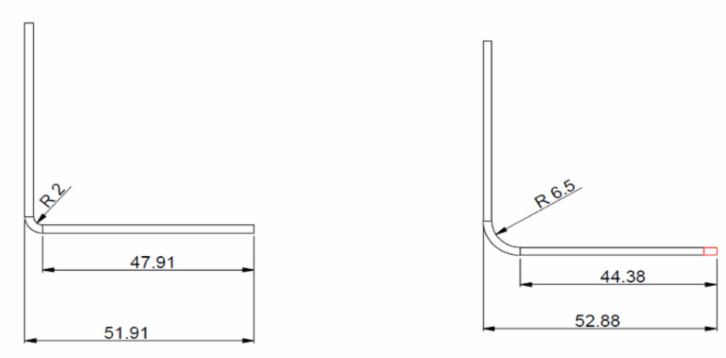
3. झुकने भत्ता
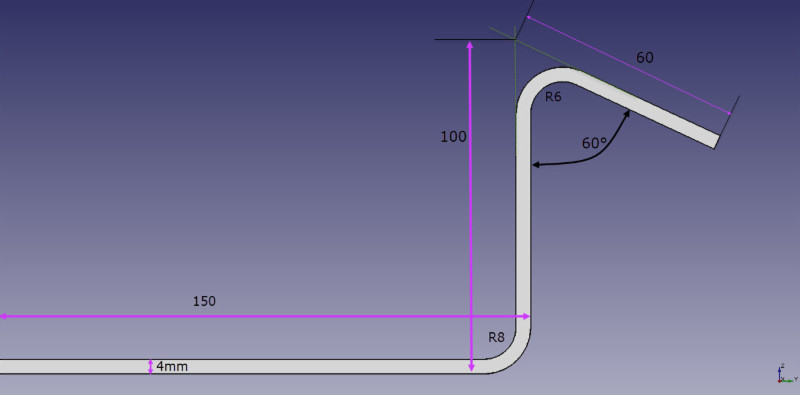
उपरोक्त आकृति के अनफोल्डेड ब्लैंक की गणना निम्नानुसार की जाएगी:
बी = 150 + 100 + 60 + बीए1 + बीए2
BA1 और BA2 की गणना कैसे करें:
झुकने भत्ते की गणना
एक बार समतल होने के बाद ओवरलैप होने पर हमें दोनों पैरों से जिस हिस्से को कम करने की आवश्यकता होती है, उसे हम आमतौर पर "बेंड अलाउंस" (या समीकरण में बीए) के रूप में जानते हैं।
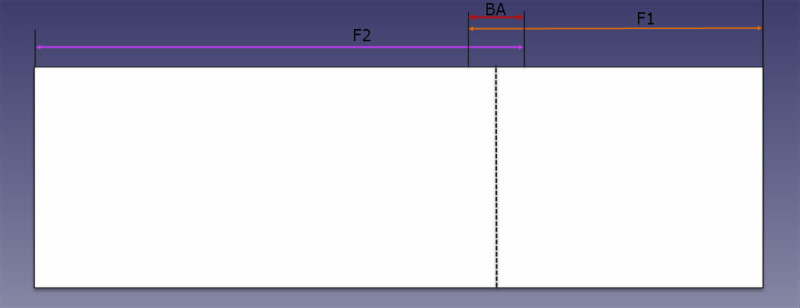
बेंडिंग अलाउंस फॉर्मूला
90° . तक झुकने के लिए BA सूत्र
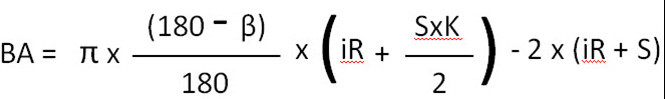
91° से 165° . तक झुकने के लिए BA सूत्र
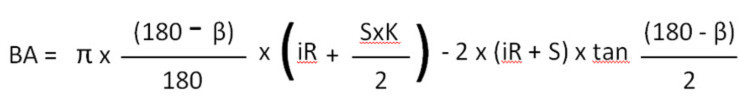
आईआर = आंतरिक त्रिज्या
एस = मोटाई
= कोण
= 3,14159265….
के = के फैक्टर
कश्मीर कारक
प्रेस ब्रेक पर झुकने पर शीट धातु का भीतरी भाग संकुचित होता है जबकि बाहरी भाग को बढ़ाया जाता है।
इसका मतलब है कि शीट का एक हिस्सा है जहां फाइबर न तो संकुचित होते हैं और न ही विस्तारित होते हैं। हम इस भाग को "तटस्थ अक्ष" कहते हैं।
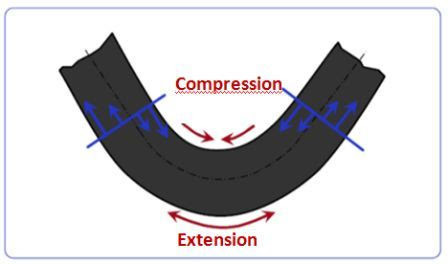
मोड़ के अंदर से तटस्थ अक्ष तक की दूरी को हम K कारक कहते हैं।
यह मान उस सामग्री के साथ आता है जिसे हम खरीदते हैं और इसे बदला नहीं जा सकता।
यह मान भिन्नों में व्यक्त किया जाता है। K कारक जितना छोटा होगा, तटस्थ अक्ष शीट की आंतरिक त्रिज्या के उतना ही निकट होगा।
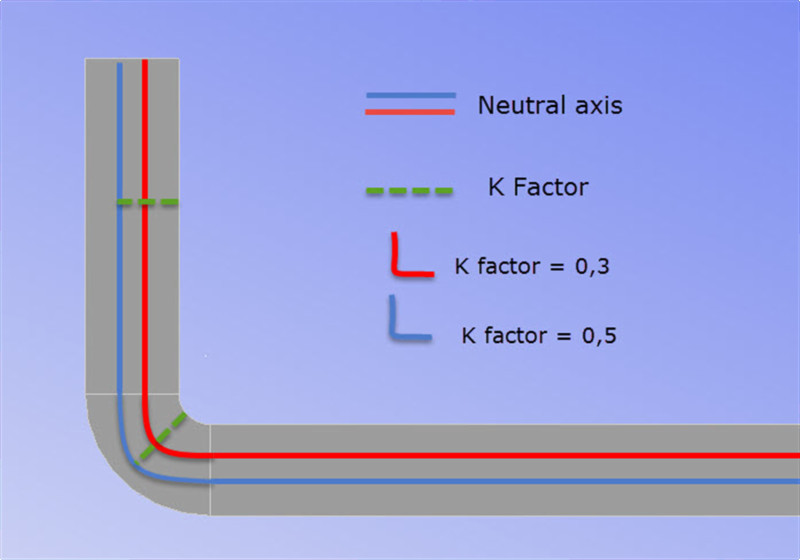
कश्मीर कारक = ठीक ट्यूनिंग
K फ़ैक्टर हमारे अनफोल्डेड ब्लैंक को प्रभावित करता है। भाग की त्रिज्या जितनी नहीं है, लेकिन हम इसे रिक्त स्थान के लिए ठीक ट्यूनिंग गणना के रूप में सोच सकते हैं।
K कारक जितना छोटा होता है, उतनी ही अधिक सामग्री विस्तारित होती है और इसलिए "बाहर धकेल दिया जाता है"…। जिसका अर्थ है कि हमारा पैर "बड़ा" हो जाएगा।
K कारक का आकलन
जब हम अपनी रिक्त गणनाओं को ठीक करते हैं तो अधिकांश समय हम K कारक का अनुमान और समायोजन कर सकते हैं।
हमें केवल कुछ परीक्षण (चुने हुए वी उद्घाटन पर) करने और भाग की त्रिज्या को मापने की आवश्यकता है।
यदि आपको अधिक सटीक K कारक निर्धारित करने की आवश्यकता है, तो आपके मोड़ के लिए सटीक K कारक निर्धारित करने के लिए गणना नीचे दी गई है।

कश्मीर कारक: एक सूत्र
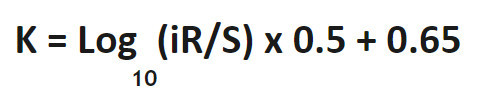
उदाहरण हल करना:
बी = 150 + 100 + 60 + बीए1 + बीए2
कश्मीर कारक अनुमान
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
दोनों मोड़ 90° या उससे कम हैं:
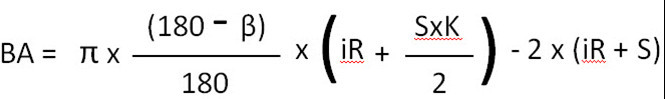
जिसका मतलब है:
बी1 = 3.14 x 0.66 x (6 + ((4×0.8)/2) - 2 x 10
बी1 = -4.25
बी2 = 3.14 x 0.5 x (8 + ((4×0.8)/2) - 2 x 12
बी2 = -8.93
इसलिए:
बी = 150 + 100 + 60 + (-4.25) + (-8.93)
बी = 296.8 मिमी